🏝️Nurikabe Map Generation with WFC algorithm

🎮Game 🧩Puzzle 🤖Algorithm 🎲PCG 💻Game Dev

Background

Logic Islands, released by sublevelgames on June 20, 2025, is a game where players place islands and walls according to predefined rule sets. The game features 6 different rule sets, and WFC was used to create stages for 3 of these rules. Today, I’d like to share the story behind this implementation.

WFC

WFC (Wave Function Collapse) is a type of PCG (Procedural Contents Generation) algorithm that analyzes the connectivity patterns of source material to generate output with identical connectivity relationships. Texture Synthesis is the general term for this technique, which creates large result images from small source images.

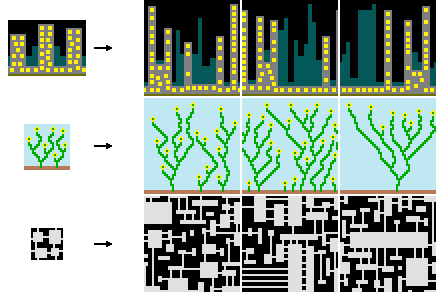
WFC creates new results based on complex connectivity relationships from the source. Since denser connectivity patterns require more computational resources, it’s better suited for generating sparse outputs. Examples include simple 2D pixel art, 3D tile models, or tile-based game maps shown in the original algorithm.

Nurikabe

Logic Islands is heavily influenced by Nurikabe published by Nikoli and the Logic Puzzles from Islands of Insight developed by Lunarch Studios. Nurikabe is a game where each cell in a grid is designated as either island or wall. Numbers in the grid indicate island sizes, each island must contain exactly one number, all walls must be connected, and no 2x2 wall blocks are allowed. Logic Islands uses these conditions as its Classic rule set.

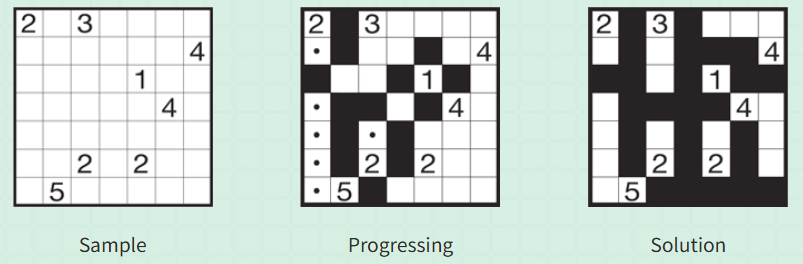
Nurikabe has many derivative rules, each existing as separate games.

Islands of Insight

Islands of Insight is a fantastic 3D game offering over 10,000 puzzles across 24 types. These puzzles require various skills including reflexes, logic, and observation. Among them, Logic Grid is a game that purely requires logical thinking. Logic Grid breaks down Nurikabe’s basic form further, creating various variations by having players complete patterns without numbers, adding exceptions to certain rules, or introducing additional rules.

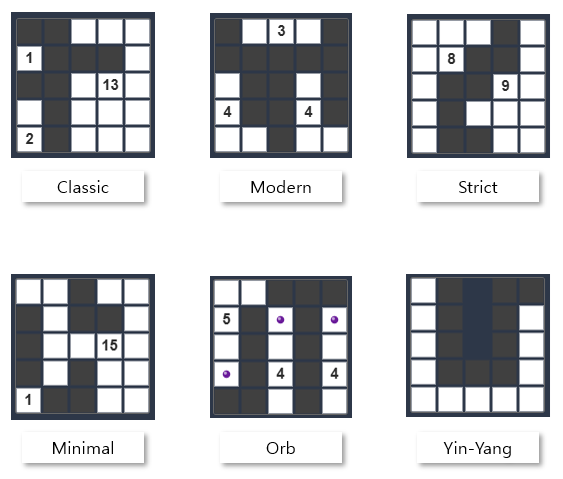
6 Rule Sets of Logic Islands

6 rules of Logic Islands are as follows:

Rule Set	Wall Connection	Island Connection	Island Separation	2×2 Walls	2×2 Islands	Special Rules
Classic	✅ Required	❌	✅ Required	❌ Forbidden	✔️ Allowed	-
Modern	✅ Required	❌	✅ Required	✔️ Allowed	❌ Forbidden	-
Strict	✅ Required	❌	✅ Required	❌ Forbidden	✔️ Allowed	Wall junction limit (3+ way connections forbidden)
Minimal	❌	❌	✅ Required	✔️ Allowed (irrelevant)	✔️ Allowed	All wall groups must be exactly 3 cells
Orb	❌	❌	✅ Required	✔️ Allowed	❌ Forbidden	- Each island needs 1 orb - Single-cell islands forbidden
Yin-Yang	✅ Required	✅ Required	❌	❌ Forbidden	❌ Forbidden	Islands without numbers allowed

Classic, as mentioned above, uses identical rules to the original Nurikabe.

Modern allows 2x2 walls but forbids 2x2 islands, creating a fresh map feel.

Strict adds wall junction restrictions to Classic - walls cannot have 3 or more neighbors - creating more constrained wall patterns.

Minimal removes the wall connectivity requirement and adds a restriction that all wall groups must be exactly 3 cells.

Orb requires each island to contain one purple orb and removes the wall connectivity requirement.

Finally, Yin-Yang removes numbers from islands but requires all walls to be connected, all islands to be connected, and forbids both 2x2 walls and 2x2 islands, creating map patterns resembling interlocking yin-yang symbols.

Problems with 3 Rules

If everything had ended after creating the map generator, there wouldn’t have been any issues. The game uses maps ranging from 4x4 to 12x12, but some rule sets had problems generating maps larger than 7x7. Modern, Minimal, and Yin-Yang were the problematic rule sets. This was something we couldn’t have known without trying.

The issue with these rule sets was their inability to generate valid wall patterns. The puzzle generation order in my generator worked like this:

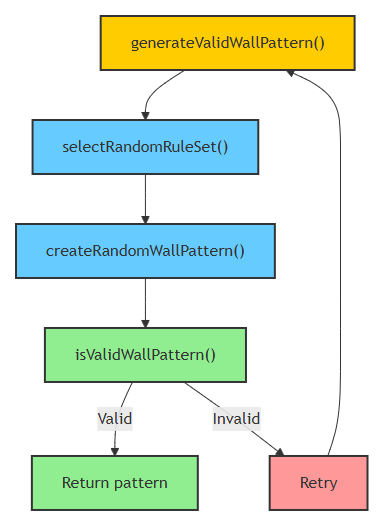
For Modern, Minimal, and Yin-Yang, I implemented wall pattern generation using WFC.

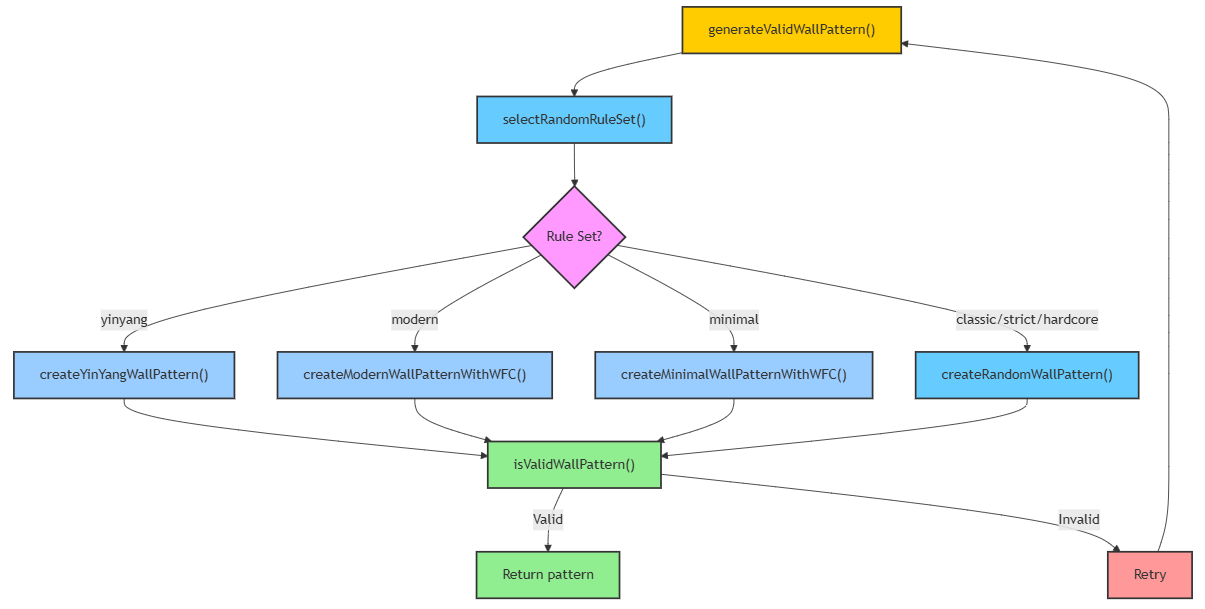
Solving Problems with WFC in Detail

When creating wall patterns with WFC, there are two crucial considerations:

• How to represent wall connectivity requirements?
• How to represent the prohibition of 2x2 walls?

If we can effectively express these two conditions with WFC, we can significantly reduce the time spent searching for random walls.

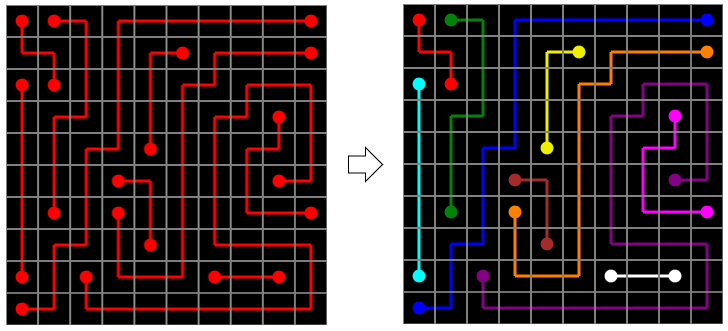
For map generation, we commonly used Simple-Tiled WFC. Unlike the more complex Overlapping WFC, Simple-Tiled WFC stores each tile and its connection information, then uses this to generate outputs. In the figure below, Simple-Tiled WFC defines 7 types of tiles (a), uses the connection relationships where roads meet non-roads (b), and generates the result (c).

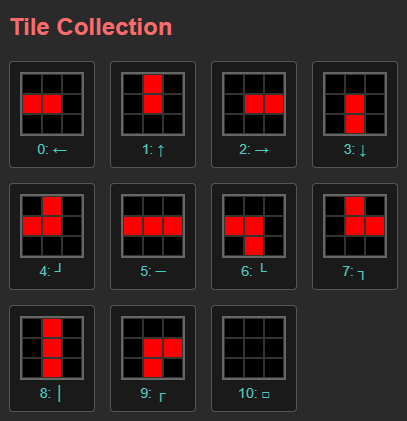
Now let’s apply this model to creating wall patterns for Logic Islands. First, we need to define tiles. The basic tiles we’ll use are these 15 types:

I defined the tiles this way because I used a similar method when creating Flow Free game maps, and it was very effective. For those interested in more details, please refer to this paper, and also check out this game and this game.

To briefly discuss Flow Free map generation, since all given node pairs must be connected and all given surfaces must be filled, we actively used constraints in WFC. After filling the entire game map, we completed the Flow Free map by giving each line a different color.

Now returning to Logic Islands, let me explain the tiles used here.

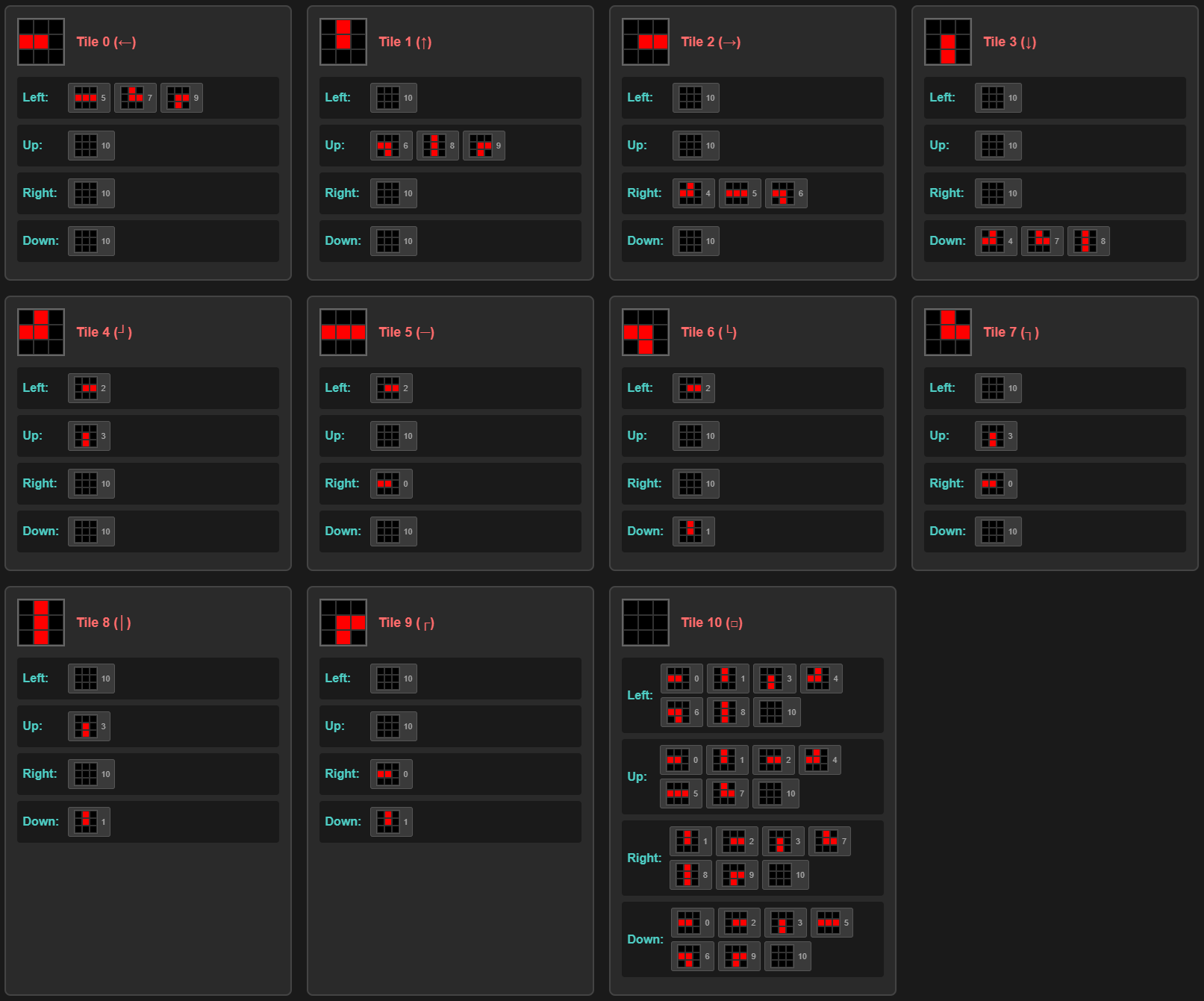
Tiles 0 through 3 are terminal nodes. They connect in only one direction, with the other three directions being empty spaces. We can represent this in data as follows:

// left, up, right, down
const tiles = {
 0: [0, null, null, null],
 1: [null, 0, null, null],
 2: [null, null, 0, null],
 3: [null, null, null, 0]
};

Tile definitions consist of 4 values per tile. Each position represents connections from the current tile in the left, up, right, and down directions. 0 indicates a connection exists and represents the first color. null means no connection.

Tiles 4 through 9 are 6 L-shaped tiles that connect in 2 directions. These can be represented in code as follows:

// left, up, right, down
const tiles = {
 ...,
 4: [0, 0, null, null],
 5: [0, null, 0, null],
 6: [0, null, null, 0],
 7: [null, 0, 0, null],
 8: [null, 0, null, 0],
 9: [null, null, 0, 0]
};

Tiles 10 through 13 are 4 T-shaped tiles that connect in 3 directions. Tile 14 is cross-shaped, connecting in all 4 directions. Tile 15 is empty space, which is essential for defining data and specifying constraints.

// left, up, right, down
const tiles = {
  ...,
  10: [0, 0, 0, null],
  11: [0, 0, null, 0],
  12: [0, null, 0, 0],
  13: [null, 0, 0, 0],
  14: [0, 0, 0, 0],
  15: [null, null, null, null]
};

Now that we’ve finished defining tiles, let’s look at connection relationships. For connections, it seems we should connect tiles that have connections with each other, and tiles without connections with each other. Following this logic, Tile 0 would meet these tiles:

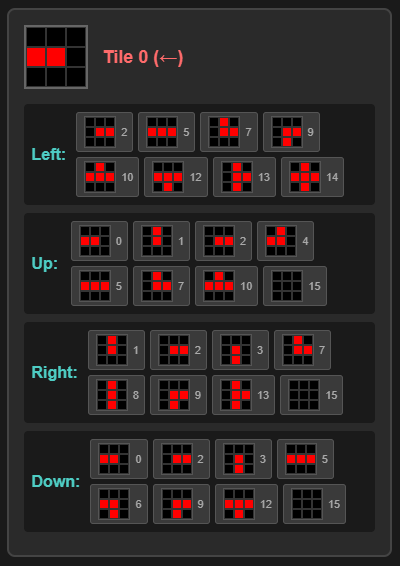
Looking at Tile 0’s connection relationships, we can see that tiles attached to the Left have connections at the center-right. The same applies to other directions.

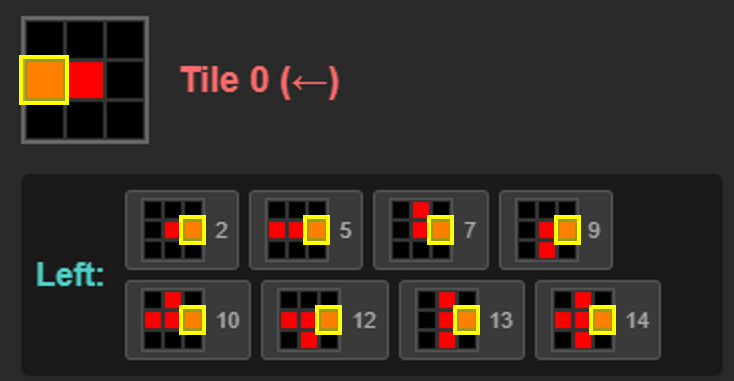
There are many tiles that can connect in each direction. However, arranging them this way makes the wall shapes too busy. The key to this map generation is to remove as much as possible from these connection relationships according to each ruleset’s conditions.

Modern

Let’s revisit the Modern ruleset:

• Wall connection required
• Island connection X
• Island separation required
• 2x2 walls allowed
• 2x2 islands forbidden

Unlike the original Nurikabe Classic rules, it allows 2x2 walls while forbidding 2x2 islands. The challenging generation condition here is whether islands can be generated to satisfy other rules while 2x2 islands are forbidden. If we can generate the most difficult part using WFC with proper constraints, we can reduce generation time. Therefore, in Modern, we generate islands, not walls, using WFC. Non-island parts will become walls in post-processing.

Lines generated by WFC become islands, where tiles with connections become islands and the rest become walls.

To ensure these connections are made correctly, first we need to prevent lines from touching each other. In other words, there should always be an empty tile (tile 15) between lines. Otherwise, lines will stick together and we won’t be able to identify island regions.

To achieve this, we need to modify tile connection relationships so that only empty tile 15 can appear in non-line directions.

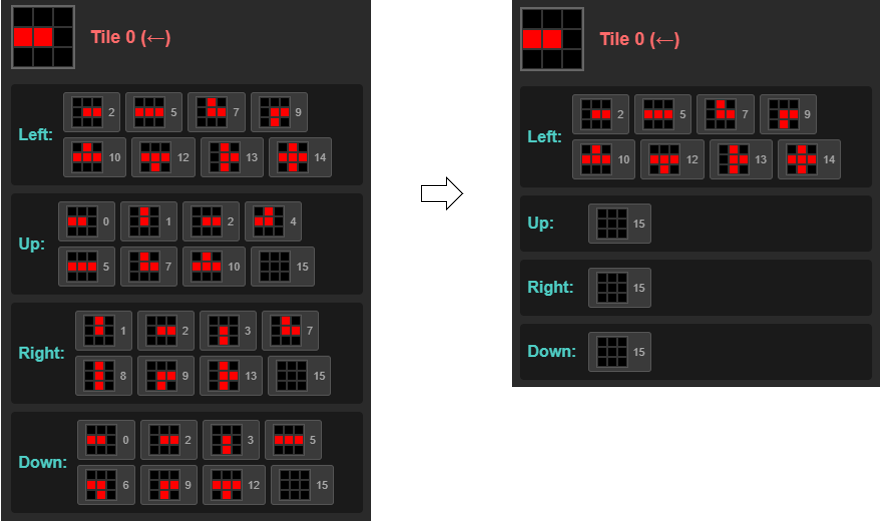
This separates islands and reduces the probability of 2x2 islands forming. Additional measures are needed to prevent 2x2 islands from forming. Specifically, we need to restrict connections between L-L, L-T, and T-T. To prevent complexity, we don’t use tile 14 (Cross). If we were to use it, we’d also need to restrict connections between L-Cross, T-Cross, and Cross-Cross.

Below are the connection relationships for tiles 4 and 10 (L tile and T tile) with these constraints applied. Tiles that can meet L and T are limited to horizontal/vertical lines and terminal nodes. Since we don’t use the Cross tile, tile 14 has been removed, and the empty tile has been renumbered from 15 to 14.

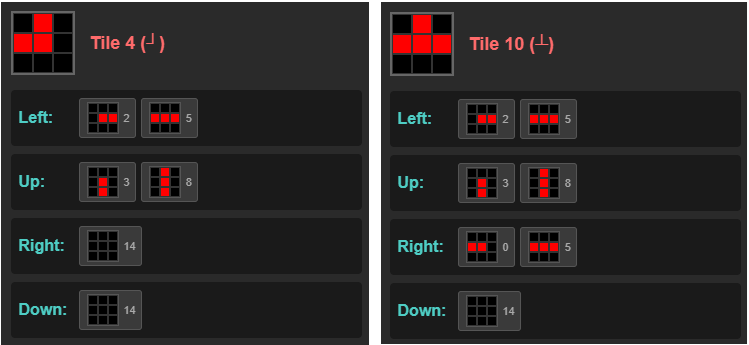
One final processing step remains. To ensure lines appear as intended, we force empty tiles to appear on the map’s outer edges - that is, cells where x=-1 || x=width || y=-1 || y=height. This way, tiles inside the map that touch the outer edges will have tiles adjacent to empty tiles, eliminating cases where lines extend outside the map and get cut off.

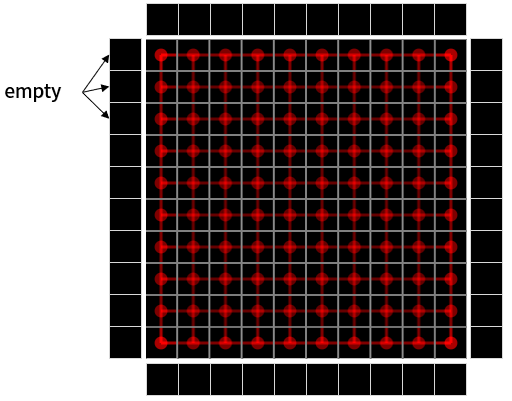
With these configured connection relationships, island patterns that match the Modern ruleset are generated well even at large sizes. While original Nurikabe only presents numbers, Logic Islands presents parts of islands and walls as fixed (green dotted lines) for easier difficulty levels.

Minimal

The Minimal ruleset is as follows:

• Wall connection not required
• Island connection X
• Island separation required
• 2x2 walls allowed (but becomes meaningless due to wall area conditions)
• 2x2 islands allowed
• Special rule: All wall areas must have size 3

Due to the special rule, all walls must have an area of 3. Areas connected by lines must equal 3, which in WFC terms means only terminal + middle node + terminal formations are possible. Here, middle nodes are L tiles, vertical lines, and horizontal lines. T tiles aren’t necessary either. Therefore, the tiles used are reduced to 11 types, fitting the name “Minimal.”

We need to prohibit unnecessary connections in the connection relationships. We prohibit terminal-terminal (because it could create 2-cell areas), L-L, L-straight line, and straight line-straight line connections, and prevent lines from touching each other like in Modern. All tile connection relationships are shown below.

With these configured connection relationships, wall patterns matching the Minimal ruleset are generated well even at large sizes. Notably, we don’t need any special processing to satisfy the special rule all wall areas must have size 3. Just through WFC’s connection relationships alone, all maps are guaranteed to have wall areas of size 3.

Yin-Yang

Finally, the Yin-Yang ruleset is configured as follows:

• Wall connection required
• Island connection required
• Island separation X
• 2x2 walls forbidden
• 2x2 islands forbidden
• No numbers on islands

Yin-Yang is the most different ruleset from original Nurikabe as islands have no numbers. Like the Eastern Taiji symbol, yin and yang are interlocked with each other.

We need 1 type each for islands and walls, and both require constraints for forbidden 2x2 walls and forbidden 2x2 islands, so this time we need to create both islands and walls as WFC lines. Since islands and walls must touch each other, we need to remove the processing that prevents lines from touching in the connection relationships.

All tiles can be used, and connections between terminal-terminal, L-L, L-T, L-Cross, T-T, T-Cross, and Cross-Cross are all forbidden.

Below are the connection relationships for tiles 4 and 10 (L tile and T tile) with these constraints applied. Compared to the Modern ruleset, the difference is that lines can attach to Tile 4’s Right/Down and Tile 10’s Down.

When generating maps according to connection relationships, more lines appear in larger maps. We then select the 2 largest areas by size and turn the rest into blocked cells to make them unmodifiable. Starting from terminal nodes, we turn a certain number of tiles into blocked cells to add randomness to the map.

Conclusion

So far, we’ve examined successful cases of using WFC to generate maps for the Modern, Minimal, and Yin-Yang rulesets in Logic Islands, which previously failed to generate maps larger than 7x7 when creating game maps with 6 different rulesets.

The key insights gained from this process are:

• Thinking about problems in reverse: In Modern, we simplified the problem by generating islands instead of walls.
• Expressing constraints as connection relationships: Complex rules like forbidden 2x2 patterns were naturally resolved just by restricting tile connections.
• Maximum effect with minimum tiles: The Minimal ruleset satisfied the challenging condition “all wall areas must be exactly 3 cells” with only 11 tiles.

WFC has shown that it can be a powerful solution for content generation in puzzle games with complex logical rules, beyond just being a tool for texture generation. While traditional backtracking methods slow down exponentially as rules become more complex, WFC could quickly generate large-scale maps with properly configured local constraints.

Logic Islands can now stably generate maps up to 12x12 for all rulesets, allowing players to enjoy the unique challenges of each ruleset across various map sizes. Through this project, I learned that sometimes looking at problems from a different angle and simply changing what we’re trying to generate can make the seemingly impossible become possible.