💣Making Explainable Minesweeper

🎮Game 🧩Puzzle 💣Minesweeper 🤖Algorithm 💻Game Dev

Background

I recently purchased and played a game called 14 Minesweeper Variants during a Steam Summer sale. It was a fun game. However, I became curious while looking at the hints provided in the game. What exactly are these?

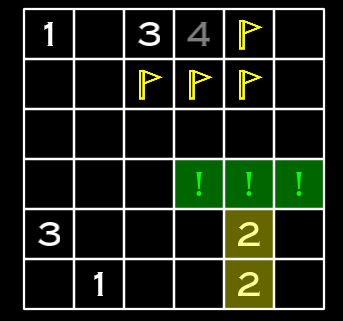
Actually, when I played Minesweeper, which was a default Windows game, I could solve cases where there was a definite answer, but I remember stepping on countless mines in ambiguous situations. For example, situations like this:

The numbers 1 and 2 indicate the number of mines in each cell’s 8 neighbors (up, down, left, right, and diagonals). Empty cells mean there are no mines in their neighbors. However, in situations like the image above, it’s not easy to figure out which squares have mines and which don’t. It’s also difficult to accurately guess the mine locations because there are too few mines.

50/50 Situations

Let’s look at this situation. This image is from this source, and it’s exactly a 50/50 probability. There’s 1 mine left, and whichever of the two remaining squares you choose, there’s a chance it could be a mine.

This situation occurs due to Minesweeper’s map generation algorithm. The original Minesweeper usually doesn’t let you step on a mine on your first click. This is because it places mines in locations other than the square the user selects on their first click. Since mines are placed at that moment, it can’t perform enough calculations to prevent 50/50 situations. When I experimented, finding boards solvable only through logical deduction required about 250,000 attempts per level on a 9x9 board with 33 mines.

Situations Where Deduction is Possible

However, there’s a common mistake that beginners like my past self often make. They think it’s a 50/50 situation and leave it to luck when deduction is actually possible! The 14 Minesweeper Variants I mentioned earlier provides hints for such situations. Let’s go back to the previous image:

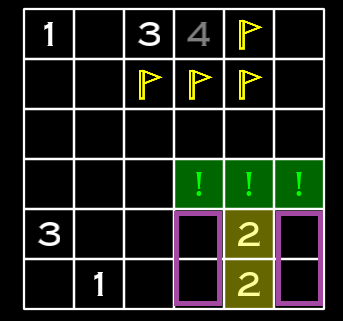
Here’s how to interpret this image. The purple square is the common area shared by the two highlighted 2 cells. The upper 2 still has 7 neighbors remaining, but the lower 2 is at the edge of the game map, so it only has 4 neighbors. Due to the existence of the lower 2, there must be exactly 2 mines in the common area. So what’s in the 3 cells above the upper 2? At least they’re not mines. That’s why those cells are safe to open.

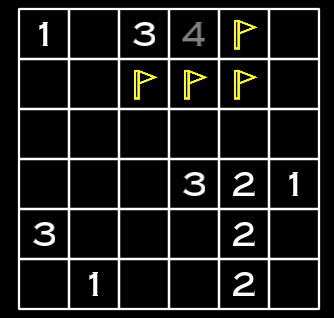
Now I’ve explained the ambiguous part. While it’s relatively easy to understand when explained in natural language like this, that game, although excellent, shows this with symbols, which took me a long time to interpret. I thought I probably wasn’t the only one. So what if there was a game that explained this in natural language? Wouldn’t it be able to show many people that they can solve more problems by making one step of deduction in Minesweeper? With this thought, I decided to create a game.

Map Generation

The maps provided in this game must be solvable only through intuitive results or deduction. To achieve this, I had the AI simulate solving puzzles from the player’s perspective and keep only the successful maps. The process is illustrated in the diagram below:

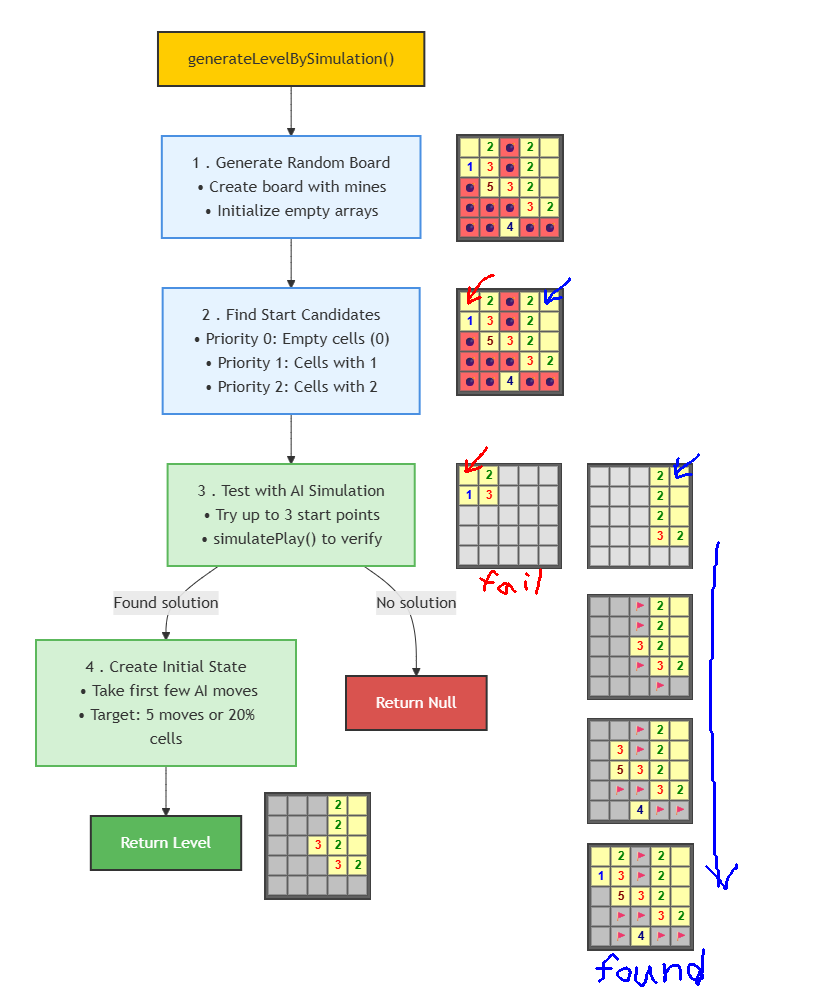
Let me explain this process step by step.

First, step 1 is generating a random board. A predetermined number of mines are randomly scattered on a board of a predetermined size.

Next, step 2 is finding candidate starting positions. Cells with values of 0, 1, or 2 are good choices, especially cells with value 0 since they also open up surrounding cells as a bonus. We find cells with values 0, 1, and 2, prioritize cells with lower values, and determine candidate starting positions. Here, only 2 candidates are shown.

Then in step 3, we actually try to solve the puzzle. At this point, the cell (0,0) marked with a red arrow gets stuck during the deduction process. It leads to the situation below:

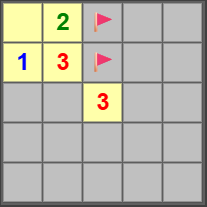
Even using all intuitive results and deduction rules, there are no certain cells. At this point, we abandon this starting point and try the next one. That’s (4,0) with the blue arrow. By solving the problem using intuitive results and deduction rules, we were able to reveal all non-mine regular cells, so this map is usable.

In step 4, we take the map found in step 3 and add some AI moves to make the map start in a slightly more revealed state than the beginning. The purpose is to make the difficulty slightly easier.

The completed level is shown below. It’s a deducible Minesweeper level that doesn’t rely on luck!

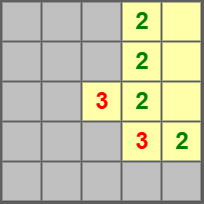
Organizing Deduction Rules

So what deduction rules were used in map generation? Since my game Explainable Minesweeper uses the same deduction rules, let me summarize what happens when you press the hint button.

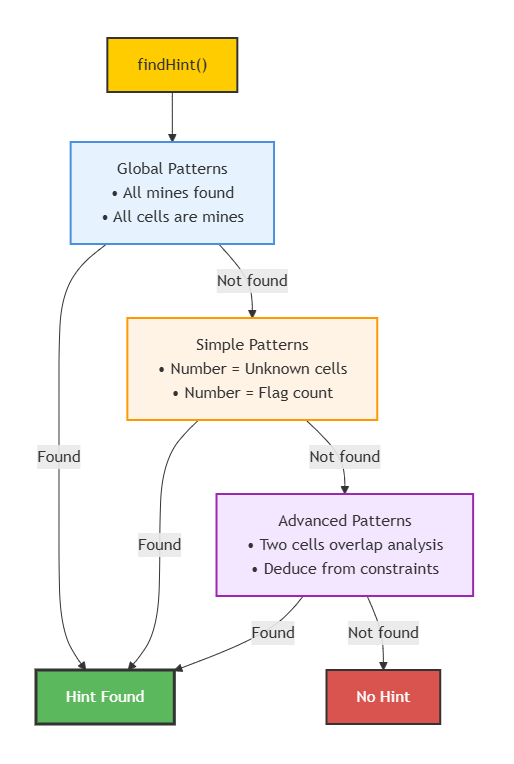
First, there are 2 Global Patterns. If you’ve found all mines, the remaining cells must all be regular cells. Or if you’ve found all regular cells, the rest must obviously be mines. Note that in my game, for logical accuracy, not only revealing regular cells but also placing flags in the wrong place results in game over.

Next, Simple Patterns are literally simple situations. When the number of unrevealed cells around a cell matches the cell’s number, you can flag all those cells. Conversely, if you’ve already placed all the flags, you can safely reveal all remaining cells.

Finally, Advanced Patterns are probably the reason I wrote this article. Along with the common area mentioned earlier, you need to consider the unique area that each cell has separate from the common area.

This pattern considers 2 numbers (note that 14 Minesweeper Variants includes patterns involving 3 or more numbers, but I excluded them as they’re too complex). When we call the first number A and the second number B, we compare the number of mines in the common and unique areas. When the difference is clear, we can determine whether the unique area is safe or contains mines.

For example, in the image below, A is 1 and B is 3. B needs 3 mines but already has 1 flagged, so it only needs 2 more. However, we cannot place 2 or more mines in the common area with A, because A must have only 1 mine as a neighbor. We also can’t place 0, because then there wouldn’t be enough spaces to satisfy B’s condition of 3 mines. Therefore, by placing 1 mine in B’s unique area (4,5) and 1 mine in one of the 2 remaining common area cells, A’s unique area becomes safe.

Conversely, here’s a case where the unique area is determined to contain mines. A has no unique area, and only B has a unique area. Since A must have 1 mine, exactly 1 must be placed in the common area, and in that case, we can see that the only option left for B’s unique area is a mine.

It’s simpler logic than you might think, right? I can’t believe I kept leaving Minesweeper to luck because I didn’t know this. Of course, there are games in the original Minesweeper where you have to rely on luck even with logical deduction. But there are no such games in Explainable Minesweeper!

Conclusion

Thank you for reading this long article. The method used here isn’t extraordinary deduction and can be thought of with common sense, but I hadn’t thought about it until now. I wrote this article and created the game thinking there might be others who could benefit like me. Since explanation is the main purpose, the game supports a total of 9 languages. If you’d like support for your language, please let me know here. And if possible, please let me know what you think about this method and the game. Thank you.